Sonia Cannas

intervalli
La scala naturale diatonica e cromatica. Per risolvere alcuni problemi della scala pitagorica nacque una nuova scala

Problemi della scala pitagorica

Abbiamo visto come si costruisce la scala pitagorica, per la precisione la scala diatonica pitagorica1. Come per ogni scala diatonica, il limitato numero di note risulta essere un limite dal punto di vista compositivo, con più note è possibile variare maggiormente le melodie. Questo svantaggio può essere superato aumentando il numero di note facenti parte della scala. Esse però non devono compromettere i vantaggi della scala diatonica, quindi devono:

  • continuare a garantire la consonanza degli intervalli di ottava e quinta2;
  • rendere il più possibile uniformi i gradi consecutivi della scala, i rapporti delle frequenze di due note consecutive devono essere costanti o al massimo solo di due tipi (cioè l’intervallo fra due note consecutive deve essere dello stesso tipo, o al massimo di due tipi diversi);
  • essere in numero non eccessivo in modo da non avere frequenze troppo ravvicinate (pensate quanti tasti dovrebbe avere un pianoforte se la scala avesse molte note).

Inserendo le note alterate che si ottengono unendo l’inizio dei due cicli di quinte ascendenti e discendenti si ottiene la scala cromatica pitagorica3:

NotaRapportoFrequenza (Hz)Cent
$\text{Do}$$1:1$$261.6$$0$
$\text{Do}_{\sharp}$$2178:2048$$279.4$$114$
$\text{Re}$$9:8$$294.3$$204$
$\text{Mi}_{\flat}$$32:27$$310.1$$294$
$\text{Mi}$$81:64$$331.1$$408$
$\text{Fa}$$4:3$$348.8$$498$
$\text{Fa}_{\sharp}$$729:512$$372.5$$612$

L’ultima colonna della tabella esprime la distanza fra le note in cent, per maggiori informazioni potete consultare la scala logaritmica.

Fra le note alterate sono state omesse quelle che nel temperamento equabile (vedi prossimo articolo) sono enarmoniche4, ad esempio è stato inserio il Do#, il cui rapporto è 2187:2048, ma non il Reb, il cui rapporto è 256:243. Contrariamente a quanto accade nelle scale basate sul temperamento equabile tali suoni non sono omofoni, cioè non sono lo stesso suono, distano un comma pitagorico5. Ciò spiega perchè un semitono pitagorico non sia la metà di un tono, e questo è uno dei problemi di tale scala. Infatti aggiungendo le note omesse la scala avrebbe 17 gradi anzichè 12, e per molti strumenti come l’arpa o il pianoforte sarebbe molto scomodo (pensate ad un pianoforte con 17 tasti per ottava…).

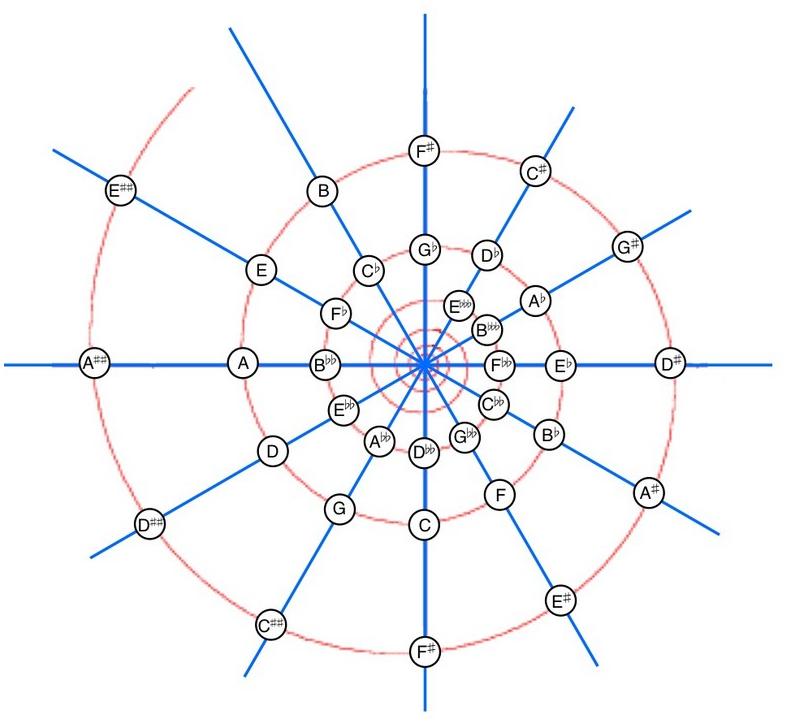
Continuando a moltiplicare o dividere la successione delle frequenze per 3/2 accade che il circolo delle quinte6 non si “chiude”, esso è in realtà un’elicoide delle quinte.

Le note rappresentanti le tonalità sono espresse secondo la notazione letterale in uso nei paesi di lingue inglese e tedesca: A=La, B=Si (per i Tedeschi B=Sib e H=Si), C=Do, D=Re, E=Mi, F=Fa, G=Sol.

Infatti se si parte da una qualsiasi nota e si sale di 12 quinte, si dovrebbe ritrovare la stessa nota 7 ottave più in alto (e quindi si formerebbe un circolo), ma seguendo il meccanismo della scala pitagorica:

129,7 = \left(\frac{3}{2}\right)^{12} \ne 2^7 = 128

Questo fatto può essere dimostrato matematicamente.

Teorema

Il sistema di intervalli ottenuto applicando il meccanismo per quinte ascendenti e discendenti non è chiuso

Dimostrazione: ricordiamo la formula della regola generativa del procedimento per quinte:

z_n = \left(\frac{3}{2}\right)^n = 2^kr_{n}, \qquad k\in\mathbb{Z}

Supponiamo per assurdo che il sistema sia chiuso.

Applicando il logaritmo in base 2 all’equazione di sopra otteniamo:

n\alpha = k + \log_2r_n, \alpha = log_2\left(\frac{3}{2}\right)
\Rightarrow \exists m,n \in\mathbb{Z}, \text{con}\, m\ne n, \text{t.c.} \, r_m = r_n
\Rightarrow m\alpha - k_1 = n\alpha - k_2 \qquad \Rightarrow \qquad \alpha = \frac{k_1 - k_2}{m - n} = \frac{p}{q}

cioè \alpha\in\mathbb{Q}. Ma allora si avrebbe:

\frac{3}{2} = 2^{\frac{p}{q}} \qquad \Rightarrow \qquad 3^q = 2^{p-q}

Quindi il primo termine è sempre dispari e il secondo pari. Ma da una qualsiasi potenza di 3 si ottiene un numero dispari, invece da una potenza di 2 si ottiene un numero pari.

Contraddizione.

Osservazione:  è un numero irrazionale.

La scala cromatica così costruita conserva la consonanza degli intervalli di ottava e di quinta, manca però la quinta Sol# – Re# poichè il Re# è stato omesso. Nel sistema temperato equabile Mib è l’enarmonico di Re#, ma nella scala pitagorica l’intervallo Sol# – Mib risulta essere dissonante. Altro svantaggio riguarda gli intervalli di sesta e terza, che continuano ad essere poco consonanti.

Tale scelta però ha il vantaggio di avere le frequenze tra due gradi consecutivi non troppo ravvicinate. Inoltre in questo modo si è riusciti ad uniformizzare sufficientemente i gradi della scala: tale uniformità è stata ottenuta inserendo le note alterate quasi a metà del tono pitagorico. Conseguentemente nella scala cromatica esistono solo due intervalli: il limma e l’apotome, la cui somma dà il tono pitagorico e la differenza il comma pitagorico.

La mancata consonanza degli intervalli di terza e di sesta rappresenta un problema non solo nella corretta intonazione di tali intervalli, ma può causare fastidiosi battimenti7 nell’esecuzione simultanea di bicordi, soprattutto in presenza di strumenti ricchi di armonici8 di ordine superiore. Il quinto armonico naturale del Do, ad esempio, viene a trovarsi molto vicino in frequenza al quarto armonico del Mi pitagorico. Se consideriamo la frequenza del Do3=261.6 Hz, il suo quinto armonico naturale avrà una frequenza pari a

261.6 \cdot 5 = 1308 Hz

Il quarto armonico naturale del Mi3=331.1 Hz avrà invece una frequenza pari a:

331.4 \cdot 4 = 1332.4 Hz

La frequenza del battimento è data dalla differenza delle due frequenze calcolate, e vale circa 25 Hz. Tale valore, secondo la teoria delle bande critiche di von Helmhotz9, cade proprio nella fascia di valori che conferiscono al suono un carattere aspro e sgradevole.

La scala naturale tolemaico-zarliniana

Un altro importante principio per dividere l’ottava in un dato numero di parti fu ideato da Archita, tarantino di scuola greca (430-348 a.C.), e fu ripreso dai greco-latini Didimo (I sec. a.C.), e Tolomeo (83-161 d.C.), ma trovò applicazione pratica solo con l’avvento della musica tonale e con la successiva teorizzazione formulata da Gioseffo Zarlino (1517-1590) nel 1558.

Mentre il sistema pitagorico prevedeva la divisione della corda in 2, 3 o 4 parti, la novità del sistema tolemaico consisteva nella possibilità di andare oltre, e quindi di dividere la corda in 5 e 6 parti.

Per dividere la corda anche Tolomeo utilizzò il monocordo: ponendo il ponticello mobile ai 4/5 della corda si ottiene (con procedura analoga a quella adottata dai pitagorici per gli intervalli di ottava, quinta e quarta) l’intervallo di terza maggiore. Detta l la lunghezza della corda:

l : \frac{4}{5} l = 5 : 4

Ponendo il ponticello mobile ai 5/6 della corda si ottiene, invece, l’intervallo di terza minore:

l : \frac{5}{6} l = 6 : 5

In questo modo anche gli intervalli di terza risultano essere consonanti, a differenza di quelli della scala pitagorica. I greci, però, ritenevano consonanti solamente gli intervalli di ottava, quinta e quarta, pertanto inizialmente questa scala non ebbe successo e non fu tramandata.

Gli altri intervalli della scala si possono ottenere come semplice interpolazione di quelli già determinati: – la seconda maggiore come differenza10 fra una quinta e una quarta giusta:

\frac{3}{2} : \frac{4}{3} = \frac{9}{8}

– la sesta maggiore come somma fra una quarta giusta e una terza maggiore:

\frac{4}{3} \cdot \frac{5}{4} = \frac{5}{3}

– la settima maggiore come somma di una quinta giusta e di una terza maggiore:

\frac{3}{2} \cdot \frac{5}{4} = \frac{15}{8}

La scala zarliniana si è imposta inizialmente per motivi legati alla maggior consonanza degli intervalli di terza. I suoni che costituiscono tale scala non hanno solo un fondamento estetico, infatti attingono dalla serie degli armonici naturali di una nota di riferimento, perciò viene detta anche scala naturale. Per la precisione essa contiene i primi 5 armonici .

Tale serie può essere generata scegliendo una nota di riferimento e moltiplicandone la frequenza per 2, 3, 4 ecc… Per riportare le note così generate nell’ambito dell’ottava di partenza si segue lo stesso procedimento visto nella costruzione della scala pitagorica: si divide la loro frequenza per 2n dove n indica il numero di ottave “percorse” dalla nota di partenza. Infine si eliminano gli eventuali “doppioni” ottenuti.

Quindi partendo dalla nota Do si ottiene:

Resta quindi il problema di decidere quante note distinte includere nella scala. La tradizione impone il numero 7 per la scala diatonica e 12 per la scala cromatica.

La scala diatonica naturale

La scala diatonica naturale in teoria dovrebbe costruirsi attingendo dalla serie degli armonici naturale le sette note prive di alterazioni. In realtà è stata costruita “ritoccando” quella pitagorica. Nella costruzione si può partire dal Mi5 che, come si può vedere dalla tabella, è il quinto armonico del Do1 la cui frequenza \nu = 261.6 Hz. Riportandolo nell’ottava di partenza si ottiene il rapporto di terza maggiore:

Mi_5 = 5\nu \quad \rightarrow \quad Mi_3 = \frac{5}{4}\nu

Partendo dal Mi3 e salendo e scendendo di una quinta (ricordando sempre di riportare le nota nell’ottava di partenza) si ottengono :

\frac{5}{4} \cdot \frac{3}{2} = \frac{15}{8} \quad \rightarrow \quad Si_3 = \frac{15}{8}\nu \\
\frac{5}{4} : \frac{3}{2} = \frac{5}{6} \quad \rightarrow \quad \frac{5}{6} \cdot 2 = \frac{5}{3} \quad \rightarrow \quad La_3 = \frac{5}{3}\nu

Possiamo riassumere i risultati ottenuti nella seguente tabella:

In questa scala si possono individuare 3 tipi di intervallo:

  • tono maggiore, che si trova fra il I e il II (fra il IV e il V e fra il VI e il VII) grado della scala, quindi il suo rapporto è:
\frac{9}{8} : \frac{1}{1} = \frac {9}{8}
  • tono minore, che si trova fra il II e il III (e fra V e VI) grado della scala, quindi il suo rapporto è:
\frac{5}{4} : \frac{9}{8} = \frac {10}{9}
  • semitono diatonico, lo si trova fra il III e il IV (e fra il VII e l’VIII) grado della scala, quindi il suo rapporto è:
\frac{4}{3} : \frac{5}{4} = \frac{16}{15}

La differenza fra tono maggiore e tono minore è di 81/80 ed è detta comma di Didimo o comma sintonico, e misura circa 21.5 cent, poco meno del comma pitagorico.

La differenza tra tono minore e semitono diatonico è di 25/24 ed è detta semitono cromatico.

La scala naturale cromatica

Il numero di note della scala naturale si stabilizzò nel Medioevo a 12. Esse si ottengono aggiungendo alle 7 note della scala diatonica naturale 5 note alterate.

La scala diatonica naturale, come ogni scala diatonica, offre un limitato numero di note, quindi una limitata gamma di possibilità melodiche. Con la scala cromatica naturale tale limite viene superato, ma le nuove note immesse non devono compromettere i vantaggi della scala diatonica. Quindi esse devono: preservare, per quanto possibile, la consonanza degli intervalli più importanti (ottava, quinta e terza);rendere il più possibile uniformi i gradi consecutivi della scala;

La scelta dei rapporti di frequenza per la costruzione della scala cromatica non è univoca. Proprio per questo nella costruzione della scala sono possibili vari criteri:

  • scegliere come semitono il semitono diatonico, pari a circa 112 cent. Utilizzando un semitono già presente nella scala diatonica, tale scelta conferisce a prima vista uniformità alla scala. Si tratta però di un’uniformità illusoria, sia a causa della differenza del tono maggiore e di quello minore, sia per la necessità di mantenere la consonanza tra gli intervalli. Ciò porta alla formazione di altri semitoni che indeboliscono l’uniformità dei gradi consecutivi della scala.
  • Un altro criterio può essere quello che si basa sul semitono cromatico.

Se si adotta come criterio di uniformità il numero di semitoni diversi contenuti nella scala, risulta essere più uniforme la scala con il semitono cromatico. Se invece come criterio di uniformità si adotta la varianza rispetto al “semitono medio” (di ampiezza 100 cent) risulta essere più uniforme la scala con il semitono diatonico.

Al di là dei diversi criteri adottati i semitoni che entrano in gioco nelle due scale sono pressoché indistinguibili all’orecchio.

Tale scala continua però ad avere gli stessi svantaggi della scala pitagorica.

Confronto tra scala pitagorica e scala naturale

Riportiamo i risultati ottenuti per la scala diatonica naturale e la scala diatonica pitagorica:

Confronto fra scala diatonica pitagorica e scala diatonica naturale. In evidenza le differenze

Dal confronto dei rapporti di frequenza si nota che quelli della scala naturale sono più semplici rispetto quelli della scala pitagorica, infatti essa prende anche il nome di scala dei rapporti semplici.

Altra differenza fra le due scale è il numero di intervalli elementari: 2 per la scala pitagorica (tono e semitono pitagorico), 3 per quella naturale (tono maggiore, minore e semitono diatonico). Nella scala pitagorica avevamo visto che componendo due semitoni successivi non si ottiene un tono. Con la scala naturale la situazione non migliora, anzi:

\frac{15}{16} \cdot \frac{15}{16} < \frac{9}{10} < \frac{9}{8}

Nonostante ciò, gli intervalli di terza e sesta della scala naturale risultano essere più consonanti, e tale consonanza è particolarmente evidente quando, su di uno strumento ricco di armonici superiori, si esegue un bicordo o più in generale un accordo: si riscontra una coincidenza di molte delle armoniche superiori che, essendo esattamente sovrapposte in frequenza, non danno luogo al fenomeno dei battimenti. Proprio per questo la scala naturale è quella che si tende ad utilizzare quando si canta ad una o più voci.

Inoltre, la scala naturale, come già visto col Mi5, contiene i primi 5 armonici naturali, a differenza di quella pitagorica che contiene solo i primi 4. Infatti in quest’ultima, partendo dal Sol3 e salendo di 3 quinte :

\frac{3}{2} \cdot \left(\frac{3}{2}\right)^3 = \frac{81}{16} < 5

Nonostante i pregi acustici della scala naturale rispetto quella pitagorica, rimangono alcuni difetti.

Infatti alcune quinte giuste tra gradi della stessa scala non risultano essere molto consonanti: la quinta Re – La ha un rapporto di frequenze pari a 40/27 < 3/2. Inoltre rimane il problema della dissonanza dell’intervallo Sol# – Mi nella scala cromatica. Questa mancata consonanza è solo un aspetto di un problema più generale: il cambiamento di tonalità. Matematicamente si potrebbe dire che le due scale sono invarianti per traslazioni, ciò significa che iniziando la scala da una nota diversa dal Do, e mantenendo le altezze dei suoni come sono state ottenute partendo dal Do, la sequenza con cui si succedono i toni e i semitoni nella nuova scala cambia completamente.

Nella musica greca tale variazione veniva utilizzata per generare i 7 modi greci, e ogni genere veniva eseguito in un solo specifico modo. Tuttavia, con l’avvento della polifonia e della musica tonale, questa proprietà non ha reso permesso la possibilità modulare da una tonalità ad un’altra. Inoltre questo risulta essere un grande limite anche per gli strumenti ad intonazione fissa (strumenti a tastiera, arpa, ecc…), infatti essi dovrebbero essere riaccordati per ogni cambio di tonalità.

Note

[1]La scala diatonica è una successione di 7 note. Per maggiori informazioni potete consultare teoria musicale: scale e intervalli.

[2]Un intervallo indica la distanza tra due note e si dice consonante quando dà una sensazione di completezza e di riposo. Per maggiori informazioni potete consultare teoria musicale: scale e intervalli.

[3]La scala cromatica è la scala che comprende tutti i suoni possibili di un sistema musicale. Nel nostro attuale sistema, basato sul temperamento equabile, è definita dalla successione di 12 semitoni contigui. Per maggiori approfondimenti potete consultare teoria musicale: scale e intervalli.

[4]Due note si dicono enarmoniche, o omofone, se hanno la stessa altezza (cioè sono lo stesso suono) ma diverso nome. Nel nostro sistema, il temperamento equabile lo sono: Do# e Re b, Re# e Mi b, Mi# e Fa, ecc…

[5]Il comma indica la differenza di frequenza tra due note di altezza quasi uguale. Per approfondimenti sul comma pitagorico si consulti la scala pitagorica.

[6]Il circolo delle quinte è una rappresentazione grafica di forma circolare in cui vengono disposte tutte le scale maggiori, con le relative minori, formate su ognuno dei 12 gradi della scala cromatica. Prende tale nome in quanto, percorrendolo in senso orario, la tonica di ciascuna scala si trova a distanza di quinta rispetto a quella della scala precedente. Per maggiori approfondimenti si consulti teoria musicale: scale e intervalli.

[7]Il fenomeno dei battimenti si verifica quando due onde (il suono è un’onda) aventi frequenze lievemente diverse si sovrappongono (ad esempio una di 440 Hz e una di 444 Hz). Per ulteriori approfondimenti si consulti http://fisicaondemusica.unimore.it/Battimenti.html.

[8]I corpi sonori non vibrano solo con la propria frequenza, detta frequenza fondamentale, ma anche con frequenze secondarie. Infatti se eccitiamo una corda fissata agli estremi, essa vibra con diverse frequenze, e tali frequenze secondarie sono multiple della frequenza fondamentale propria della corda. In generale gli strumenti musicali, a differenza di quelli elettronici, producono suoni non puri, e ciò è casuato proprio dalla sovrapposizione delle diverse armoniche, infatti oltre al suono fondamentale si sviluppano i suoni armonici, che si fondono con esso. Un orecchio umano allenato può riuscire a sentire i primi armonici, ma l’ampiezza diminuisce sempre più, pertanto da un certo punto in poi diventano impercettibili. Tutto ciò viene spiegato matematicamente nell’analisi di Fourier.

[9]Una banda critica è un intervallo di frequenze entro alla quale due toni puri simultanei non possono essere percepiti come distinti.

[10]Per differenza si intende la differenza fra i logaritmi delle frequenze. Analogamente per somma si intende il prodotto fra i logaritmi delle frequenze. Per un maggior approfondimento si veda la scala logaritmica.

Bibliografia

AA. VV., Enciclopedia della musica, Le Garzantine, Garzanti libri, gennaio 1999.

AA. VV., Dizionario Enciclopedico della Musica e dei Musicisti, Torino, Utet.

N. Chiriano, Pitagora e la Musica, Alice \& Bob, Centro Pristem Un. Bocconi (http://matematica.unibocconi.it/articoli/pitagora-e-la-musica) – n. 15, dicembre 2009.

Fisica Onde Musica, (http://fisicaondemusica.unimore.it/).

S. Isola, Temperamenti: matematica e teoria musicale, (http://www.unicam.it/).

scarica il file dell’articolo

Scala_naturaleDownload
Spread the love