
Carlo Ubertone e Nino Martino
Dalla proprietà della proporzionalità di g rispetto all’inverso del quadrato della distanza discende il teorema di Gauss. In questa prima parte si definisce il flusso di un vettore attraverso una superficie qualunque attraverso una superficie chiusa
Definizione di flusso di un vettore attraverso una superficie qualunque
Facciamo un’ulteriore generalizzazione. Come possiamo definire il flusso di un vettore attraverso una superficie qualunque? Supponiamo che il campo vettoriale non sia nemmeno uniforme. In ogni punto della superficie il vettore cambia e cambia la sua direzione, e la superficie ha una forma qualunque.
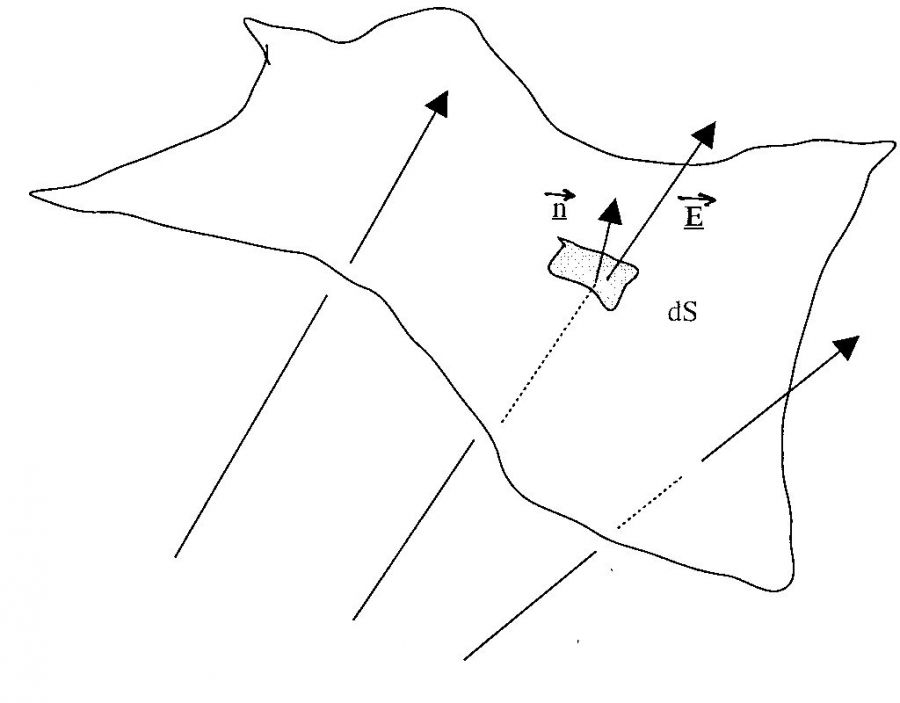
Noi avevamo definito il flusso di un vettore attraverso una superficie piana, ma la superficie in figura non è certamente piana. E poi NON siamo in presenza di un campo uniforme.
Ricorriamo allora a un “trucco”, del tutto identico a quello che userete in analisi matematica, prossimamente (è il concetto alla base).
Prendiamo un elemento infinitesimo di superficie \(dS\). Un elemento infinitesimo è un elemento piccolo, più piccolo di ogni numero preso piccolo a piacere. Ma è zero? NO, non è zero. È più piccolo di 1mm2? Sì. È più piccolo di 0,000001mm2? Sì. È più piccolo di 0,000001mm2? Sì. Ma è zero? NO, non è zero. Ecco, questo è il trucco.
Ma l’elemento di superficie \(dS\) è così è piccolo che possiamo pensarlo come un infinitesimo di superficie piana. Ma se faccio la somma infinita (infinita!) di tutti gli elementi infinitesimi di superficie piana ottengo la superficie di partenza, che NON è piana..Cosa ho ottenuto con questo “trucco”?
Ho ottenuto che ora posso scrivere la mia definizione precedente di flusso attraverso la superficie piana.
L’elemento infinitesimo (infinitesimo!) di flusso è dato ora dalla formula:
$$d\varPhi(\vec{A})=\vec{n}\cdot\vec{A}dS$$
Il vettore \(\vec{A}\) lungo tutta l’elemento infinitesimo di superficie è costante in modulo, direzione e verso. Non fai n tempo a cambiare.
E ovviamente \(\vec{n}\) è il versore per dare il carattere vettoriale all’elemento di superficie infinitesima \(ds\), come fatto in precedenza. Il suo verso anche qui è arbitraria, in qualche modo, ma vederete in seguito che l’arbitrarietà si scioglierà.
Il flusso totale attraverso la superficie totale \(S\) sarà allora la somma infinita (infinita!) di tutti gli infinitesimi di flusso:
$$\varPhi_{S}(\vec{A})=\sum_{\infty}d\varPhi(\vec{A})$$
Noi abbiamo usato il segno di sommatoria per indicare la somma infinita di infiniti infinitesimi. In realtà poi vedrete in matematica che questa particolare somma si chiama “integrale” e si scrive con un apposito simbolo: \(\int\)
Quindi la formula in termini matematici più compatti si scriverà:
$$\varPhi_{S}(\vec{A})=\int d\varPhi(\vec{A})$$
Come vedete stiamo costruendo passo passo il formalismo necessario per arrivare al teorema di Gauss che poi sarà assai semplice simbolicamente, sfrutterà a pieno le proprietà del campo vettoriale gravitazionale e che ci permetterà di calcolare in maniera rapida una serie di situazioni che altrimenti sarebbero estremamente complicate. Ci stiamo costruendo lo strumento matematico per semplificarci la vita, non certamente per complicarcela ( si spera).
E ora facciamo un ultimo passo:
Definizione di flusso di un vettore attraverso una superficie chiusa qualunque
Adesso è semplice definire il flusso del vettore \(\vec{A} attraverso una superficie chiusa. Un esempio di superficie chiusa potrebbe essere la superficie di una sfera. Un esempio di superficie qualunque aperta potrebbe essere una lamiera ondulata.
In realtà nella formula non c’è niente da cambiare. La superficie S che figura al pedice del flusso è la superficie chiusa. Ma la cosa interessante è che possiamo sciogliere l’ambiguità del versore \(\vec{n}\). Convenzionalmente si definisce il verso positivo del versore \(\vec{n}\) quello che punto fuori della superficie chiusa, come verso negativo del versore \(\vec{n}\) si assumerà quello che punta dentro la superficie chiusa:
$$\varPhi_{S}(\vec{A})=\int \vec{n}\cdot\vec{A}dS$$
Abbiamo qui usato il simbolo \(\int \) al posto di \(\sum_{\infty}\) per correttezza formale. Il significato è chiaro e per quello che ci servirà non sarà necessario studiare a fondo le proprietà degli integrali, o saperli calcolare.
- la gravitazione – introduzione
- la forza di gravità
- le tre leggi di keplero
- proprietà del campo vettoriale gravitazionale
- energia potenziale e funzione potenziale nel campo gravitazionale.
- energia potenziale e funzione potenziale, forza gravitazionale e campo gravitazionale
- teorema di gauss per il campo gravitazionale – parte prima
- teorema di gauss per il campo gravitazionale – parte seconda
- teorema di gauss per il campo gravitazionale – parte terza

