una prima rielaborazione delle misure di aerea

Nino Martino, Carlo Ubertone

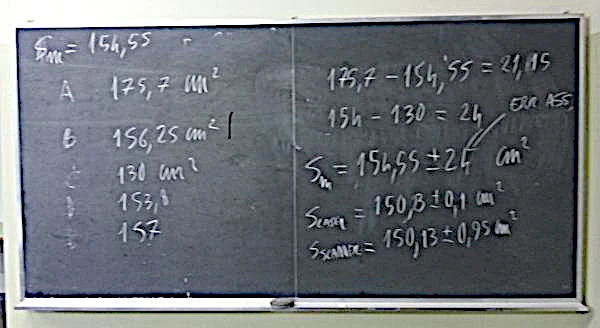
Dai dati delle misura di un’area irregolare forniti dai vari gruppi inizia una prima elaborazione rudimentale della teoria degli errori. Sviluppi ulteriori di teoria degli errori saranno fatti in occasione di un altro esperimento condotto in laboratorio. La teoria della misura e l’elaborazione delle incertezze (sarebbe meglio chiamarla così invece di “teoria degli errori” viene introdotta in questo modo a passi successivi, con livelli di astrazione sempre crescenti, si arriverà ad usare un foglio di calcolo a computer, con impostate le formule più evolute. Difficile dimenticare, in questa maniera. Quindi, in ultima analisi, si risparmia un sacco di tempo..

Nella foto della lavagna sono riportati i valori delle misure dell’area irregolare.

gruppo A:  175,7 cm²

gruppo B:  156,25 cm²

gruppo C:  130 cm²

gruppo D:  153 cm²

gruppo E:  157 cm²

I metodi usati per determinare la misura dell’area sono stati fondamentalmente tre:

1. La figura irregolare veniva riportata su un foglio di carta quadrettata tracciandone il contorno. Poi veniva disegnato un rettangolo che la conteneva, poi venivano contati i quadretti tra il rettangolo e l’area da misurare, poi si sottraeva dall’area del rettangolo il numero di quadretti contati e si otteneva così il numero di quadretti dell’area da misurare. Ciascun quadretto era mezzo cm. .
2. Si riportava la figura su un foglio quadrettato e si contavano i quadretti dentro al contorno della figura.
3. Si pesava un quadrato della stessa carta della figura da misurare, “abbastanza” grande, si pesava la carta della figura e poi si faceva la proporzione: peso figura : peso quadrato=area figura : area quadrato

I risultati sono differenti tra di loro. Qual è la misura “vera” dell’area irregolare? Gli studenti hanno risposto che non esiste una misura vera, ci sono misure approssimate. Perché? Per esempio, hanno detto, è difficile apprezzare il quadretto, bisogna decidere quando contare un quadretto se la linea del contorno lo attraversa (per eccesso o per difetto? e quando l’uno e quando l’altro?). Il gruppo che ha effettuato la pesata ha ammesso che anche il loro metodo non poteva dirsi preciso, la bilancia ha una sua precisione (Si è in grado di valutare quanto? E in che modo?). Aggiungiamo, noi, che ci sono anche altri errori non considerati nella misura con il peso: ad esempio sull’area del quadrato campione pesato. Il quadrato è stato ritagliato con una forbice, la stessa misura del quadratino è fatta con una riga di inchiostro che ha un suo spessore. Per quanto possiamo aumentare la precisione della nostra misura non possiamo essere certi in modo assoluto del uso valore.

Alcuni hanno proposto id usare un laser (evidentemente nell’immaginario collettivo il laser è cosa assai precisa) con un apparato non meglio determinato. Ma anche il raggio laser ha un suo spessore, pur sottile. E se si usasse uno scanner riportando poi la figura a schermo del computer e usando un programma per calcolarne l’area? nessuna speranza: lo schermo ha una risoluzione in pixel determinata, e il programma ha la sua incertezza. Non c’è alcuna possibilità di effettuare una misura “esatta”. Immaginate: è come riportare la figura che avevate su carta millimetrata. Ma la linea del tracciato di contorno passa comunque sempre all’interno di un quadratino più piccolo, un millimetro di lato, e dovete comunque sempre approssimare.

Questa questione della misura esatta impossibile è generale, non è collegata alla misura specifica di una area.

La misura fisica di qualunque grandezza che incontreremo in seguito sarà sempre approssimata, magari in modo eccellente, mai esatta. Ma questo, al di là dell’apparenza, non creerà troppi problemi, vedrete.

Si è chiesto allora come si può fare. Quale sarà il valore della misura più … verace, attendibile. Scartata l’ipotesi di prendere uno dei cinque valori come esatto (ciascun gruppo sosteneva a gran voce la bontà della … propria misura…) avete convenuto che magari si poteva fare una media:

(misura₁+ misura₂ + misura₃ + misura₄ + misura₅)/5

È la media aritmetica tra tutte le misure. Il risultato l’avete calcolato:

S_m=154,55 cm²

Adesso il problema è capire quanto sia “buono” questo valore.  Sappiamo che c’è sicuramente un errore, che c’è una “incertezza”. Come stimare questo errore, questa incertezza? A qualcuno di voi è venuta l’idea di prendere la differenza fra la media e il valore più alto e la differenza fra la media e il valore più basso. Sembra ragionevole.

175,7 – 154,55 = 21,15

e

154-130 = 24

Se prendiamo la differenza maggiore sembra ragionevole dire che la misura dell’area (almeno rispetto alle misure effettuate) è :

154 cm² ± 24 cm²

Se io prendo il valore 154, tutte le mie misure cadono nell’intervallo centrato su 154 e che ha per ampiezza 24.

Il numero 24 cm² lo chiameremo d’ora in poi errore assoluto. Niente di particolare, è un nome come un altro, l’abbiamo costruito insieme e quindi avete il concetto, per non ripetere lunghi discorsi diciamo “errore assoluto” e tutti capiscono a che cosa si riferisce. Ci stiamo costruendo insieme un linguaggio, quello scientifico che ha una apparenza normale, ma che ha significati propri comprensibili e comuni a tutta la comunità scientifica (niente di filosofico, niente attribuzione di valore etico, l’errore è una incertezza e non consiste in un qualche cosa di profondamente sbagliato  e eticamente assai riprovevole, e “assoluto” non c’entra niente con la ricerca disperata dell’assoluto, tranquilli…).

Se noi raffiniamo le nostre misure, ad esempio con il computer, o con il laser o con altro, troveremo altri numeri per la mia area. Per esempio potremmo trovare:

S_laser = 150,3 cm²± 0,1 cm²

S_scanner = 150,13 cm²±0,95cm²

I numeri sono ovviamente inventati. ma la cosa interessante che con un po’ di tempo e attrezzature avremmo potuto verificare è che le misure con minore errore assoluto sono contenute sempre dentro le misure con maggiore errore assoluto. E’ la vita 🙂

Ma come possiamo costruire un indice della bontà della nostra misura? E’ evidente che se commetto un errore di 24 cm² misurando una area di 150 cm² o se commetto un errore sempre di 24 cm² misurando 10.000 m² di terreno (un ettaro…), mi trovo in due situazioni completamente differenti. Tutti concordate che la seconda misura ha una precisione quasi impossibile! Lo stesso “errore assoluto” incide percentualmente molto ma molto di meno nel secondo caso.

Nel primo caso ho fatto un errore del 16%

Nel primo caso un errore del 2,4 ·10^-7 % (assurdamente piccolo)

Il numero che si ottiene dividendo l’errore assoluto per il valore della misura si chiama errore relativo (e si può esprimere in percentuale moltiplicando il risultato per 100).

Abbiamo aggiunto al nostro vocabolario scientifico un altro termine, per parlare velocemente e sinteticamente tra di noi senza possibili ambiguità del linguaggio comune (e anche questa volta non c’è niente di filosofico, niente cose del tipo: ah, tutto è relativo, ciascuno la pensi come vuole tanto l’ha detto Einstein con la relatività, e altre stupidaggini del genere…).

Ma adesso per concludere poniamo una questione. Ma tutte le misure all’interno dell’intervallo tra la media e lo scarto massimo o minimo hanno la stessa probabilità? Nel senso: se io faccio altre misure otterrò altri valori, ma sono sparpagliati in modo casuale o ci sono misure che sono più probabili, che si otterranno più probabilmente? Come si distribuiscono i valori delle misure di una grandezza quando faccio molte misure? E quante misure debbo fare per avere risultati attendibili?

E’ quello che svilupperemo prossimamente e useremo excel (o equivalente) per trattare molti dati (ecco perché l’avete appreso in laboratorio informatico…). Ma cambieremo la grandezza da misurare.

Avete impiegato circa un’ora per misurare una semplice area. Per avere una decina di misure, migliorando le prestazioni, potreste impiegare sei-sette ore passate a contare quadretti. Semplicemente letale.

Cambieremo la misura, misureremo cose la cui misura richiede poco tempo. E introdurremo nuove cose, (e nuovi termini scientifici…). E vedremo che in effetti si può pensare a una incertezza della misura assai più ristretta di quella trovata con le nostre precedenti cinque misure. Le misure non hanno tutte la stessa probabilità… E’ importante capirlo e saperlo, per poter fare previsioni (che credete? Le compagnie di assicurazioni giocano sempre a loro vantaggio…).

I nuovi termini introdotti:

errore assoluto: simbolo Δx (dove x è il simbolo della misura da effettuare,nel nostro caso avremmo scritto ΔS)

errore relativo: simbolo ε_r

Prossimamente su questi schermi termini come:

scarto quadratico medio (AAAARRRRGGGHHH!!!)

sigma (basta così!…)

e altre cose del genere.

Queste cose le introdurremo solo quando saranno necessarie e non prima.

Piano complessivo:
Alla ricerca del metodo
la misura di una area di forma irregolare – Premessa
la misura di una area di forma irregolare – Laboratorio
la misura di una area di forma irregolare – Elaborazione misure
oggetti che cadono e metodo scientifico
gli oggetti cadono anche a Zuoz (Svizzera)
Osservare e studiare l’oscillazione di un pendolo
Il pendolo in laboratorio
Il pendolo in laboratorio – punto della situazione
Prima o poi arriveremo da qualche parte
Trattamento dati con excell
Teoria e link vari
Il fenomeno dell’elasticità prima lezione
il fenomeno dell’elasticità report di laboratorio
il fenomeno dell’elasticità e le grandezze proporzionali
gli elastici sono veramente elastici?
… e via via altro ancora…